1. Introduction

quation of the surface on the trapezium-curved plan, coefficients of quadratic forms of the surface.

The orthogonal curved system of coordinates at the plane there is formed by the system of the straight lines orthogonal to the plane base curve ( ) ( ) ( )j i r u y u x u + = 0 (Fig. 1).

So, the curved-orthogonal coordinates there are organized by the system of the equidistant curves parallel to the based curve and the system of the straight lines orthogonal to the system of the equidistant curves.

The equation of the curved coordinate system

( ) ( ) v u v , u ? ? = 0 r r ,(1)

? is a normal to the base curve, v is the coordinate of the generating curves along the normal to the base curve.

The positive direction of the coordinate of straight lines there is taken to the side of the convexity of the base curve, because in the direction of the concavity the straight lines may to cross.

Assigning some function of vertical coordinate z(u,v), we receive the vector equation of the surface ( ) v , u ? on the base curved-orthogonal coordinate system at the plane

( ) ( ) ( )k r v , u z v u v , u + ? = ? 0 ? . (2)

For deduction the formulas of the coefficients it's necessary to receive the derivatives of the vector equation and to use the formulas of the classic differential geometry [2];

? s? = ? 0 r ; 0 r? = ? s ; ? ? s k k s = ? = ? ? ; k s k s ? = ; ? s k ? = ? ? . (3)

Then receive:

( ) The coefficients of the first fundamental forms:

k u s u z vk s + + ? = ? ? ; k v v z + ? = ? ? . (4)( ) ( ) 2 2 u s u u z vk s E + + ? = = ? ? ; ( ) 2 1 v v v z G + = = ? ? ; ( ) v u v v z z F = = ? ? . (5)

The unit normal vector of the surface

( ) ( )( ) ( ) k m + + ? ? ? = × ? = ? ? ? ? v s u v ? z vk s z 1 1 ,(6)( ) ( ) ( ) 2 2 2 2 1 u v s v ? z z vk s F EG + + + ? = × = ? = ? ? ? is a discriminant of the surface.

The second derivatives of the equation:

( ) ( ) k uu s s s uu z k vk s k v s + + ? + ? + ? ? = ? ? ? ; k uv s uv z k + = ? ? ; k vv vv z = ? . (7)

The coefficients of the second fundamental form:

( ) ( ) ( ) ( ) ? + ? ? + ? + ? + ? ? = = uu s v s s u s uu z vk s z k vk s z k v s L 2 m ? ; ( ) ( ) ? + ? = = vv s vv z vk s N m ? ; ( ) ( ) ? + ? ? ? = = uv s s u uv z vk s k z M m ? . (8)

The curvatures of the surface:

( ) ( ) ( ) ( ) [ ] 2 2 2 u s uu s v s s u s u z vk s z vk s z k vk s z k v s E L k + + ? ? + ? ? + ? + ? + ? ? = = ; ( ) ( ) 2 1 v vv s v z z vk s G N k + ? + ? = = ; ( ) ( ) [ ] ( ) 2 2 2 1 v u s vv s s u uv z z vk s z vk s k z EG M k + + + ? ? + ? ? ? = = . (9)

The coordinate system of the investigated surfaces isn't orthogonal and isn't conjugated in common, as the coefficients 0 ? M , F and the coordinate system of the surfaces isn't the lines of principle curvatures of the surface.

The investigated system of the surfaces is related to the class of normal surfaces [4][5][6] -the surfaces with the system of plane coordinate lines (generating curves) at the normal plane of the directrix curve. At the works [4,5] there was shown, that only for two kinds of normal surfaces the system of generating curves is the system of principle curvatures: 1-surfaces of rotation -directrix is a straight line, generating lines are circles; 2 -normal surfaces with the system of nonchanged generating curve. This type of surfaces is related to the Monge's surfaces [5,[7][8][9][10].

If z=z(v) -the generating curve doesn't change during moving in normal plane of the directrix (z u =z uu =0), there will be received the Monge's surfaces:

( ) 2 s vk s E + ? = ; ( ) 2 1 v v v z G + = = ? ? ; 0 = F ; ( ) 2 1 v s z vk s + + ? = ? ; ( ) 2 1 v v s s z z k vk s L + + ? = ; 2 1 v vv z z N + = ; 0 = M ; ( ) 2 1 1 v s v s z vk s z k k + + ? == ; ( ) 2 3 2 2 1 / v vv z z k + = . (10)

The coordinate system of the Monge's surfaces is lines of principle curvatures of the surface.

If the generating curve will be a straight line ? = vtg z (? is an angle of slope of generating strait line to the plane of base curve), then there will be received the torus surface of constant slope [10][11][12]. Then we'll receive:

? = tg z v ; 0 = vv z ; ? = + 2 2 1 1 cos z v ; ? + ? = ? cos vk s s ; ( ) 2 s vk s E + ? = ; ? = 2 1 cos G ; ( ) ? + ? = sin k vk s L s s ; N=0; s v s vk s sin z k k + ? ? == 1 ; k 2 =0. (11)

If the angle of slope of the generating strait line ?=0, z=0, then will be received the trapezium-curved plate:

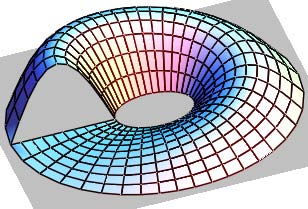
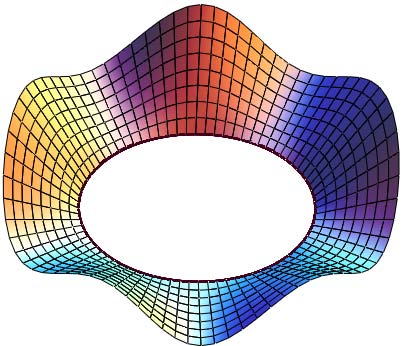
( )2s vk s E + ? = ; 1 = G ; L=N=0; k 1 =k 2 =0. (12)

The geometric characteristics of surfaces with concrete directrix and generating curves will be received on the base of the common formulas of coefficient of the surfaces on trapezium-curved plans (3)(4)(5)(6)(7)(8)(9)(10)(11). On the fig. 2 there is shown the surface with ellipse as directrix and generating sine with linier change of its amplitude:

( ) ( ) ( )j i r u Y u X u + = 0 ; ( ) u cos a u X = ; ( ) u sin b u Y = ; ( ) d v sin u c v , u z ? ? = 2 ; ? ÷ = 2 0 u ; d v ÷ = 0

, c is maximum amplitude of sine curve; d is the width of trapezium curved plan.

Determine parameters of the directrix ellipse and derivatives of generative curve:

? = ? + ? = ? a Y X s 2 2 ; u cos u sin 2 2 2 ? + = ? ; a b = ? ; ? ?? = ? ? 2 a s ; ( ) u sin 2 1 2 ? + = ?? ; 2 3 3 / a s Y X Y X k ? ? = ? ? ? ? ? ? ? ? = ; ? ? = ? = k s k s ; ( ) 2 2 2 2 1 ? ? + ? ? = ?? ? ? ? = ? u sin k s ; d v sin c z u ? ? = 2 ; 0 = uu z ; d v cos d c z uv ? = 2 ; d v cos u d c z v ? = 2 ; d v sin u d c z vv ? ? ? = 2 2 .

2. Coefficients of the fundamental forms:

v sin c v a E ? ? + ? ? ? ? ? ? ? ? ? ? + ? = 2 2 2 2 4 ; d v cos u d c G ? + = 2 2 2 2 4 1 ; d v sin u d c F ? ? = 2 8 2 ; d v sin c d v cos u d c v a ? ? + ? ? ? ? ? ? ? ? ? + ? ? ? ? ? ? ? ? ? ? + ? = ? 2 2 2 2 2 2 2 2 4 4 1 - ( ) ? ? µ ? ? ? ? ? ? ? ? ? ? ? + ? + ? ? ? ? ? ? ? ? ? ? ? + ? ? + = = 2 2 2 2 1 2 2 2 d v cos u d v a d v sin u sin v u sin a c L s uu m ? ; ? ? ? ? ? ? ? ? ? ? ? ? + ? ? ? = d v sin u v a d c N 2 2 ; ? ? ? ? ? ? ? ? ? ? ? ? + ? + ? ? ? ? ? = 2 1 1 d v cos v a d d v sin c M . (12)

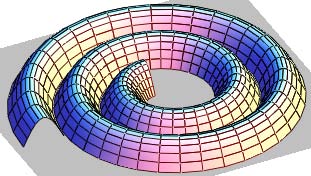
On the fig. 2 there is shown the Monge's surface with evolvent of the circle as directrix:

( ) ( )

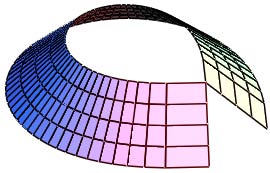
u sin u u cos a u X + = ; ( ) ( ) u cos u u sin a u Y ? =d v cos d b G v v 2 2 2 1 + = = ? ? ; ( ) d v cos d b v au 2 2 2 1 + + = ? ; ( ) d v cos d b d d v cos v au b L 2 2 2 1 + + = ; d v cos d b d d v sin b N 2 2 2 2 1 + ? = ; ( ) d v cos d b v au d d v cos b k 2 2 2 1 1 + + == ; 2 3 2 2 2 2 2 1 / d v cos d b d d v sin b k ? ? ? ? ? ? ? ? + ? = . (13)

On fig. 4 there is shown the torus surface of constant slope with Bernoulli's lemniscate as directrix:

( ) ( ) u cos u aR u X = ; ( ) ( ) u sin u aR u Y = ; ( ) u cos u R 2 2 = , ( )41 1 / u ? ÷ ? = . ( ) u R a s 2 = ? ; ( ) a u R k 2 3 = ; 3 = s k .

The coefficients of fundamental forms and the curvatures of the surface:

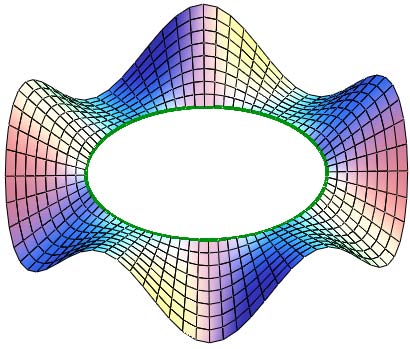
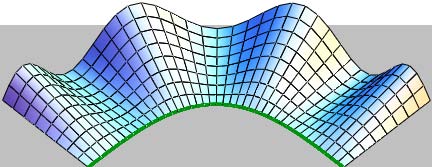
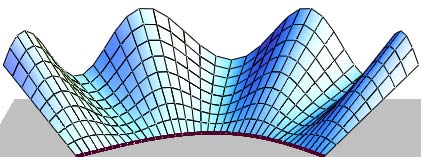
( ) 2 3 2 ? ? ? ? ? ? ? ? + = v u R a E ; ? = 2 1 cos G ; ( ) ? ? ? ? ? ? ? ? ? + = sin v u R a L 3 2 3 ; ( ) ( )v u R a sin u R k 3 2 3 1 + ? = ; 0 2 = k . (14)

Let us consider the linier surfaces which aren't surfaces of constant slope. On fig. 5 there are shone wavy linear surfaces with different directrix curves.

? + + ? ? ? ? ? ? ? ? + ? ? ? ? ? ? + = ? ( ) ( ) ( ) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? + ? + ? ? ? ? ? ? + + = 1 2 2 2 2 2 2

3. Conclusion

The surfaces on the trapezium curved plans are formed by the moving of some generating curve at the normal plane of directrix curve. The generative curve may change its form when it is moving along the directrix, but has the constant wide of the plan. At the article there is received the vector equation of the surfaces on trapezium curved plans. On the base of the vector equation there are received the coefficients of the fundamental forms and the curvatures of the surfaces. If the function of vertical coordinates depends on coordinate parameter of the directrix (the form of generating curve changes at moving along the directrix), then the coordinate system of the surface isn't orthogonal and isn't conjugated. If along directrix there moving unchangeable curve then the coordinate lines of the surface are lines of principle curvatures and this type of surfaces is applied to the class of Monge's surfaces [5,[7][8][9]. On the base of common formulas there are received the formulas of geometric characteristics of the Monge's surfaces. If at the normal plane of the directrix there is moving a straight line with the constant slope to the directrix plane, then there will be received the torus surface of constant slope. Those type of surfaces belong to the class of Monge's surfaces as well.

On the base of common formulas of investigated class there are received the formulas of the surfaces and their geometric characteristics of the surfaces with concrete directrix and generating curves, as for surfaces of common type and so for Monge's and surfaces of constant slope. The using of common formulas made more simple the proses for receiving formulas for concrete surfaces. For every investigated surface there are given their figures.

Also there was investigated the type of wavy surfaces formed by the generating straight line which make oscillations at the normal plane of directrix. There are received the formulas of the geometric characteristics of this type of surfaces and given the figures of wavy line surfaces with some directrix lines.

The figures of the surfaces were made with using of vector equations of the surfaces in the "MathCad" system [5,13]

Fig. 1: Pseudo-polar coordinate system — Figure 1. Fig. 1 :

Fig. 2: Surface with ellipse directrix and sine generating curve — Figure 2. Fig. 2 :

is an amplitude of the sine, d is width of the sine (surface). Parameters of directrix and generating curve: — Figure 4. b

Coefficients of the fundamental forms: — Figure 5. .

Fig. 3: Evolvent-sine Monge's surface — Figure 6. Fig. 3 :

Fig. 4: Lemniscate surface of constant slope — Figure 7. Fig. 4 :

Appendix A

Appendix A.1

The generating straight line at its moving along directrix made a wavy motion at the normal plane of the directrix: a) ( ) ( ) The coefficients of the fundamental forms and curvatures of these surfaces are determined on common formulas (4-9) with using formulas (19) and the fact that N=0, k v =0. If to take cycloid as the directrix (fig. 5,d

Appendix B

Ð?"???????? ? ???????????????? ???????????? ???????????????? ??????????? ?? ?????? ?????????? ??????????? ????????????. ???????????? ???????? ?????????? ??????????? ? ??????????, ? ? ?????? , ? ? ??????? . p. .
Lectures on the Differential Geometry of Curves and Surfaces, A R Forsyth . 1920.
Surfaces Given with the Monge Patch in E4E4. B Bulca , K Arslan . Jour. Math. phis., Analit., Geom 2013. 9 (4) p. .
Application of analysis to Geometry, G Monge . 1936. Moscow, ONTI.
Geometry of ruled surfaces with cuspidal edge and the linear theory of analysis of torus shells, S N Krivoshapko . 2009. (357 p)
Encyclopedia of Analytical Surfaces, S N Krivoshapko , V N Ivanov . 2015. Springer International Publishing Switzerland. (752 p)
Classical differential Geometry, V I Shulikovskiy . 1963. Moscow, GIFVL. 540.
Orthogonal Curved Coordinate System and Forming the Surfaces on Trapezium-Curved Plans, V N Ivanov , T S Imomnazarov , I T Farhan . 10.22363/2312-8143-18-4-518-527. http://journals.rudn.ru/tnginttring-researches p. . Vestnic of Russian Friendship University. Ser.: Engineering Investigations (T. 18. -? 4)
Comparative analysis of the results of determining the parameters of the stress-strain state of equal slopes shell, V N Ivanov , O Alyoshina .
Geometry of Monge surfaces and construction of the shells// Structural mechanics of engineering constructions and buildings/ Mezhvuzovskie sbornic of science works. V N Ivanov , Rizvan Muhammad . Vip. 11. -Moscow: Izd-vo ASV, 2002. p. .
Geometry and forming of the normal surfaces with system of plane coordinate lines. V N Ivanov . Structural mechanics of engineering constructions and buildings, 2011. p. .
Constructive forms of space constructions. V N Ivanov , V A Romanova . Visualization of the surfaces at the systems "MathCAD", and "AutoCAD". -Monograph. -Moskow: Izd-vo ASV, 2016. (412 p)
Constructing shells and their visualization in system. V N Ivanov . 10.1088/1757-899X/456/1/012018. IOP Conference Series: Materials Science and Engineering 2018) 012018, 2019. 456. (MathCad" on basis of vector equations of surfaces)

Geometrical Characteristics of the Surfaces on Trapezium-Curved Plans

Table of contents